La définition de Illusion

L'illusion désigne un phénomène manifestant une discordance entre une expérience perceptive et des propriétés physiques de la stimulation.

Les caractéristiques des illusions

Classiquement, les illusions sont décrites comme des erreurs, des perceptions qui ne correspondent pas à la réalité, comme une tromperie de nos sens. Elles existent dans toutes les modalités sensorielles. Pour des auteurs comme James Gibson, elles sont des épiphénomènes, des curiosités de laboratoire. Pour les gestaltistes, au contraire, elles reflètent les contraintes structurales des stimulations. De tout temps, elles ont été utilisées comme arguments venant à l'appui des théories de la perception ou étant en contradiction avec elles. L'extrême variété des mécanismes en jeu dans les illusions entraîne qu'il n'en existe pas de théorie générale. Les illusions sont des témoins de l'activité perceptive et s'expliquent donc au même tire, et dans les mêmes cadres théoriques, que les phénomènes non illusoires.
La notion d'illusion est à mettre en regard de l'idée d'une perception correcte des propriétés physiques des stimulations. Les relations géométriques dans des dessins au trait ont été le plus souvent étudiées. Dans ce cas, une illusion se traduit par un désaccord entre les propriétés géométriques perçues et celles qui ont été définies lors de la construction de la figure. Il y a donc non-concordance entre une définition a priori du stimulus, définition qui est de nature cognitive, et l'interprétation de l'information sensorielle réalisée par les traitements perceptifs. De ce point de vue, les illusions ne sont pas essentiellement des erreurs, mais bien des témoins des mécanismes de traitement.
En effet les illusions reflètent d'abord la manière dont l'organisme traite des informations sensorielles et par là nous permettent de mieux définir l'information réellement traitée par le système sensoriel. Néanmoins, les variations des illusions avec différents facteurs comme l'âge, l'expérience, le contexte, significatif ou non, suggèrent une importante participation des représentations cognitives.

Les illusions optico-géométriques

Cette expression est la traduction de l'expression proposée par Johann Oppel: geometrisch-optische Täuschung. Beaucoup de ces illusions ont été décrites au XIXe siècle par des auteurs allemands dont elles portent le nom. L'expression désigne les illusions observées dans des dessins au trait et portant sur des propriétés géométriques des figures: longueur ou orientation de segments, taille et forme de surfaces.
Pour chaque illusion, on distingue une partie déformée sur laquelle porte l'illusion, et un déformant, qui provoque l'illusion. Toutes ces illusions révèlent des interactions spatiales entre des éléments présentés simultanément dans le champ visuel. Les effets consécutifs figuraux peuvent être considérés comme des illusions dans lesquelles le déformant et le déformé sont présentés successivement. Le sens des déformations est souvent inverse entre les illusions (simultanées) et les effets consécutifs.

Les illusions de longueur de segments

La longueur apparente de deux segments de droite ou de deux intervalles spatiaux (déformé) de même orientation et d'égale longueur physique est modifiée par le contexte pictographique dans lequel sont présentés ces segments.
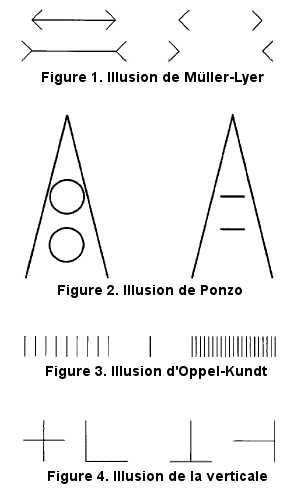Dans l'illusion de Müller-Lyer (Figure 1), le sens de l'ouverture des terminaisons en forme de pointes de flèches (pennures) engendre l'illusion. Ainsi, le segment terminé par des pennures internes paraît plus court que le segment terminé par des pennures externes.
Dans l'illusion de Ponzo (Figure 2), l'inégalité apparente de la longueur des segments horizontaux est obtenue par leur insertion entre deux lignes convergentes. Ainsi, le segment horizontal situé plus près de l'apex de l'angle de convergence paraît plus long que celui qui en est plus éloigné.
Dans l'illusion d'Oppel-Kundt (Figure 3), le segment hachuré paraît plus long que le segment vide de hachures. L'espacement des hachures, et donc leur nombre, modifie l'amplitude de l'illusion.
Dans l'illusion de la verticale (Figure 4), l'orientation des segments est la cause d'une illusion de longueur. Ainsi, la verticale paraît plus longue que l'horizontale. Le type de connexité des deux segments module l'amplitude de l'illusion, qui croît des figures de gauche à celle de droite. La verticale à prendre en considération est la verticale égocentrique et non la verticale gravitaire.

Les illusions de surface

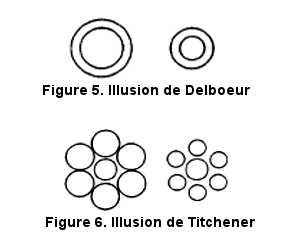Dans l'illusion de Delboeur (Figure 5), la surface apparente d'un disque diminue lorsque ce disque est entouré d'un cercle plus grand, et augmente lorsque le cercle déformant est à l'intérieur.
Dans l'illusion de Titchener (Figure 6), les deux disques déformés sont entourés par une couronne de disques déformants. Ainsi, le disque entouré d'une couronne de gros disques paraît plus petit que le disque entouré d'une couronne de petit disques.
Ces illusions ne résultent pas que d'effets de contraste entre la taille des disques déformés et celle des disques déformants. En effet, l'augmentation de la proximité relative des éléments déformants peut suffire à augmenter la surface apparente comme dans la forme de l'illusion de Ponzo avec des disques (Figure 2). L'illusion de la lune à l'horizon consiste dans le fait que la lune apparaît plus grosse lorsqu'elle est située près de l'horizon qu'à son zénith. Elle souligne aussi l'importance de la proximité de références spatiales dans l'estimation de la surface. De plus, cette illusion fait intervenir des représentations de la distance et donc des mécanismes de constance des grandeurs.

Les illusions d'angles et d'orientation

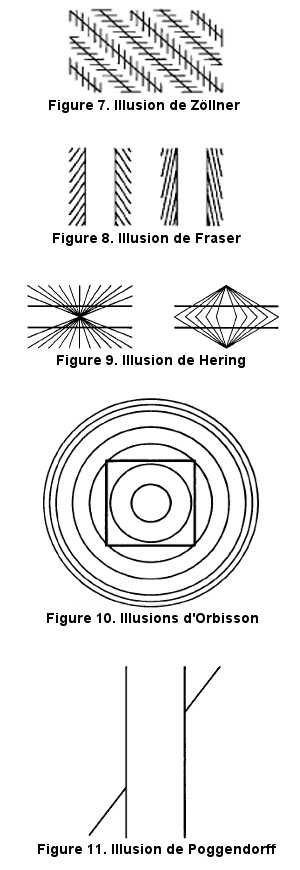Dans l'illusion de Zöllner (Figure 7), une série de lignes parallèles est hachurée de segments courts d'orientation différente et orthogonale d'une ligne à l'autre. Les lignes n'apparaissent plus parallèles. Si les lignes déformées ont une orientation de 45°, les lignes hachurées de segments horizontaux auront une orientation apparente plus proche de la verticale et les lignes hachurées de segments verticaux auront une orientation apparente plus proche de l'horizontale.
Si l'angle formé par les lignes et les segments qui les hachurent diminue, l'illusion diminue. Elle s'inverse, comme dans l'illusion de Fraser, pour des angles inférieurs à 10° (Figure 8).
Dans l'illusion de Hering (Figure 9), deux lignes droites et parallèles tracées sur un fond de lignes convergentes ou divergentes apparaissent déformées, soit de manière convexe, soit de manière concave. Cette illusion peut être considérée en partie comme une variante de l'illusion de Zöllner.
Les illusions d'Orbisson utilisent comme déformant soit une figure faite de cercles concentriques (Figure 10), soit une figure faite de rayons à l'intérieur d'un cercle. Les déformés sont soit des lignes parallèles comme dans l'illusion de Hering, soit des carrés, des cercles ou des triangles.
Dans l'illusion de Poggendorff (Figure 11), les deux moitiés d'un segment oblique masqué en partie par deux verticales parallèles n'apparaissent plus alignées. L'effet semble double. D'une part, il porte sur l'angle apparent, qui paraît plus aigu qu'il n'est. D'autre part, il semble y avoir un déplacement de l'apex de l'angle, qui augmente la distance entre les deux angles et entraîne une perte de l'alignement apparent.
Ces illusions ont en commun de montrer une augmentation de l'angle apparent séparant deux segments. C'est pourquoi on les qualifie souvent d'effets de contraste. Lorsque, comme dans les illusions de Hering et d'Orbisson, les angles formés par le déformant et le déformé varient progressivement, la perception est celle d'une ligne incurvée. La grandeur des effets diminue lorsque le déformé est orienté verticalement ou horizontalement.

L'interprétation théorique des illusions optico-géométriques

Depuis l'origine, l'explication des illusions a donné lieu à des débats acharnés. Cependant, aucune théorie ne réussit à expliquer toutes ces illusions, et encore moins toutes leurs variations. On admet que plusieurs ordres de facteurs doivent être invoqués pour expliquer de manière satisfaisante les illusions. Schématiquement, les explications actuellement plausibles des illusions optico-géométriques invoquent trois ordres de mécanismes.

• Les premiers types de mécanismes: il s'agit de mécanismes neurosensoriels précoces, automatiques, coderaient une information différente de celle qui résulte de la description géométrique des figures. Dans ce cadre, il n'y a pas à proprement parler d'illusions, mais ces phénomènes sont les révélateurs privilégiés des caractéristiques de ces traitements précoces. Ainsi, l'illusion de Müller-Lyer résulterait fondamentalement du fait que l'information sensorielle sur la longueur repose sur l'activité des neurones dont le champ récepteur est activé par les figures. Or, celles-ci englobent nécessairement les pennures. Les neurones activés par la figure à pennures externes auront des champs récepteurs de plus grande taille que ceux qui sont activés par la figure à pennures internes.
  D'autres illusions s'expliquent par la sélectivité des neurones visuels à l'orientation ou à la taille (fréquence spatiale). Dans ces cas, il existe des interactions inhibitrices entre neurones codant des orientations ou des tailles voisines qui rendent compte des effets de contraste mentionnés.
  
  
• Les seconds types de mécanismes: ils font appel aux activités exploratoires des individus, qu'il s'agisse, soit de mouvements oculaires, soit de déplacements de l'attention. Toutefois, ces illusions sont obtenues pour des durées de présentation brèves et, de ce fait, ne permettent pas leur exploration.
  
  
• Les troisièmes types de mécanismes: il s'agit des mécanismes de constance de taille. Plus précisément, à la suite d'Armand Thiéry, Richard Gregory fait l'hypothèse que de nombreuses illusions sont le résultat de l'interprétation des projections planes de figures tridimensionnelles. Les mécanismes de constance de taille interviendraient ici pour fournir une échelle de référence. Tout élément suggérant une perspective comme dans la figure de Müller-Lyer (Figure 1) interviendrait pour activer une représentation tridimensionnelle dotée de constance. En conséquence des effets de profondeur ainsi créés, la taille apparente des objets lointains apparaîtrait plus grande que celle des objets proches lorsque ces deux objets sont de même taille physique.

Pour élucider les mécanismes en jeu, diverses approches ont été mises en œuvre: des études psychophysiques dans lesquelles on fait varier les différentes dimensions des figures (par exemple, les angles des segments et des lignes dans l'illusion de Zöllner), des études développementales, des comparaisons interethniques, des études portant sur les effets de l'exercice, des études portant sur des animaux. Ainsi, les études des différences de grandeur des illusions entre groupes ethniques ont été effectuées avec des objectifs contradictoires: soit montrer l'importance de variables proprement culturelles et donc fortement cognitives, soit montrer l'influence de variables environnementales conditionnant la maturation des systèmes sensoriels. Les Européens ont une illusion de Müller-Lyer plus forte que les autres groupes, mais une illusion de la verticale moins forte. Les effets de l'environnement ne sont pas démontrés de manière convaincante. Par contre, les effets de l'éducation apparaissent plus notables sans pouvoir, et de loin, expliquer toutes les différences.
Très généralement, les illusions optico-géométriques tendent à diminuer en amplitude avec des présentations répétées. Pour l'essentiel, cet effet de l'exercice ne dépend pas de la connaissance que l'individu peut avoir de l'illusion. Si une illusion peut être transitoirement réduite, voire annulée, au cours d'une session d'exercice, elle réapparaîtra chez ces individus lors de sessions ultérieures. Les illusions résistent à la connaissance que l'on peut avoir de leurs effets.
Par ailleurs, les études comparatives faites sur les animaux suggèrent certes qu'ils peuvent avoir des illusions, mais ces études sont insuffisantes pour permettre des comparaisons valides avec ce qui est observé chez les humains.

Les illusions de profondeur et de distance

Dans cette catégorie, on trouve essentiellement des figures donnant une impression de profondeur.
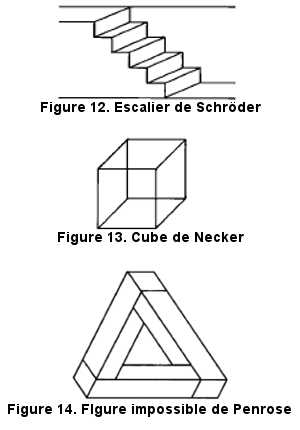En fait, on pourrait dire que toute représentation bidimensionnelle donnant une impression de profondeur et de relief est une illusion ou un ensemble d'illusions. Dans certaines de ces figures dessinées, les perspectives apparentes sont réversibles comme l'escalier de Schröder (Figure 12) ou le cube de Necker (Figure 13) en raison de l'instabilité apparente de leurs faces.
La profondeur relative des faces de l'objet n'est pas constante. Lors d'une observation prolongée, les deux perspectives possibles alternent assez régulièrement. On attribue cette alternance au fait que le stimulus ne comporte pas assez d'indices qui permettent de trancher entre deux hypothèses structurales qui se trouvent être de fait aussi plausibles l'une que l'autre. L'augmentation du nombre et de la qualité des indices picturaux de profondeur diminue les possibilités de réversibilité.
D'autres figures, comme celles proposées par Penrose (Figure 14), sont dites impossibles. Ce sont bien évidemment les objets qu'elles représentent qui sont impossibles. Elles sont réalisées par des combinaisons d'indices picturaux de la profondeur.

Les illusions de mouvement

Le mouvement des objets est à la fois cause et objet d'illusions.
En ce qui concerne les illusions dues au mouvement, une transformation continue d'une silhouette ou d'un contour peut dans certaines conditions donner lieu à la perception du mouvement d'un objet en profondeur. C'est l'effet cinétique de profondeur, étudié, soit à partir de l'ombre projetée d'un objet réel, soit au moyen du mouvement de points ou d'éléments sur un écran graphique. Ainsi, une surface carrée augmentant régulièrement en taille est perçue comme s'approchant de l'observateur. La perception anorthoscopique consiste dans le fait que la vision successive et ordonnée des différentes parties d'une figure défilant derrière une étroite ouverture permet de percevoir, dans certaines conditions de rapidité, l'ensemble de l'objet. En somme, perceptivement, il est possible de faire passer un chameau par le chas d'une aiguille!
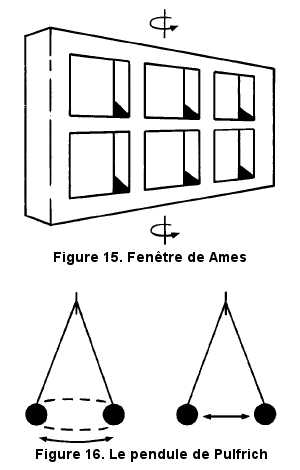En ce qui concerne les illusions portant sur le mouvement, une surface de forme trapézoïdale, dite fenêtre de Ames (Figure 15), mise en rotation autour de son axe vertical engendrera la perception d'un mouvement oscillant et non celle d'un mouvement circulaire régulier. Dans le phénomène du pendule de Pulfrich (Figure 16), on observe le mouvement de va-et-vient d'un objet, exactement comme les oscillations d'un pendule, en portant devant un filtre qui a pour effet d'atténuer la lumière, mais le mouvement perçu est celui d'une rotation en profondeur. Au lieu de percevoir les oscillations dans un plan, on percevra un mouvement de rotation du pendule en profondeur.
Le phénomène peut être observé avec un téléviseur. En effet, le bruit visuel qui remplit l'écran quand le canal du récepteur n'est pas réglé donne l'impression de deux mouvements de sens opposés vus en transparence. Les impressions de profondeur résultent des écarts temporels entre les informations visuelles des deux yeux. Les informations de l'œil portant un filtre sont retardées. La combinaison binoculaire des informations entraîne des modifications de la profondeur apparente.

Les illusions de contraste

Ce sont des phénomènes liés à l'intégration de plusieurs niveaux de luminance et dans lesquels le contraste apparent diffère du contraste physique local.
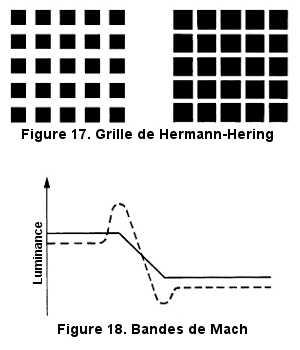Dans la grille de Hermann-Hering (Figure 17), on perçoit aux intersections de la grille des taches plus sombres (figure de droite). L'illusion s'inverse lorsque la grille est faite de barres noires sur fond blanc (figure de gauche). Elle est attribuée au fonctionnement antagoniste des régions on et off des champs récepteurs.
Les bandes de Mach (Figure 18) sont des phénomènes de rehaussement de contraste apparaissant à la limite de deux surfaces de luminance différente. Du côté de la surface claire, on perçoit une bande plus claire que le reste de la surface et, du côté de la surface sombre, une bande plus sombre (en traits pleins, la variation physique de la luminance entre une région claire et une région sombre; en pointillés, la luminosité). Là encore, les neurones visuels sensibles au contraste seraient responsables de cet effet.
Le terme d'illusion couvre un vaste ensemble de phénomènes très hétérogènes. N'ont été mentionnées ici que des illusions visuelles. Toutes comportent de multiples variantes. Aucune théorie proposant un mécanisme unique ne peut expliquer totalement les effets. Les illusions perçues résultent de l'action de plusieurs niveaux de traitement. Nombreuses sont celles qui sont déjà présentes dès le niveau des codages sensoriels, c'est-à-dire au niveau auquel peut être définie l'information sensorielle réellement disponible. Il reste que ces informations seront intégrées dans des représentations qui peuvent conduire à des remaniements.

L'évolution des illusions optico-géométriques avec l'âge

On sait depuis longtemps que l'intensité d'une illusion varie avec l'âge de l'individu ou avec la répétition des mesures.
Les illusions optico-géométriques primaires sont considérées par Jean Piaget comme des effets de champ primaires, déterminés par les propriétés physiques des figures stimulus. Les premières recherches ont fait apparaître dans presque tous les cas une diminution du degré d'erreur avec l'âge. L'usage de méthodes de mesure plus rigoureuses, appliquées à des populations nombreuses, réparties en classes d'âge étroites, y compris des enfants très jeunes, a permis de mettre en évidence que l'illusion augmente avec l'âge avant de diminuer. La forme générale de l'évolution est une courbe à maximum, en U renversé. Le maximum d'erreurs ne se situe pas au même âge pour toutes les illusions: entre 9 et 11 ans pour l'illusion d'Oppel et celle du parallélogramme de Sanders, à 7 ans pour l'illusion de Poggendorff, 5 ans pour celle de Müller-Lyer. Toutefois, il y a quelques exceptions. En effet, l'illusion de Ponzo augmente jusqu'à 7 ans sans décroître ensuite et celle de Titchener augmente de 9 à 19 ans. Pour Robert Pollack, le maximum d'erreur pourrait coïncider avec le sommet de la courbe de maturation des récepteurs sensoriels. Le maximum devrait alors se situer au même âge pour toutes les erreurs primaires. Or, ce n'est pas le cas...
Les illusions optico-géométriques secondaires sont caractérisées par le fait qu'elles apparaissent et croissent sous l'influence d'activités perceptives (polarisation, transport) qui engendrent des effets de champ nouveaux, dits secondaires (effets sériaux, anticipations, schématisations, polarisations, effets de cadre, etc...). La théorie des centrations relatives de Piaget est un modèle particulièrement adapté à l'interprétation des effets de champ, aussi bien secondaires que primaires.